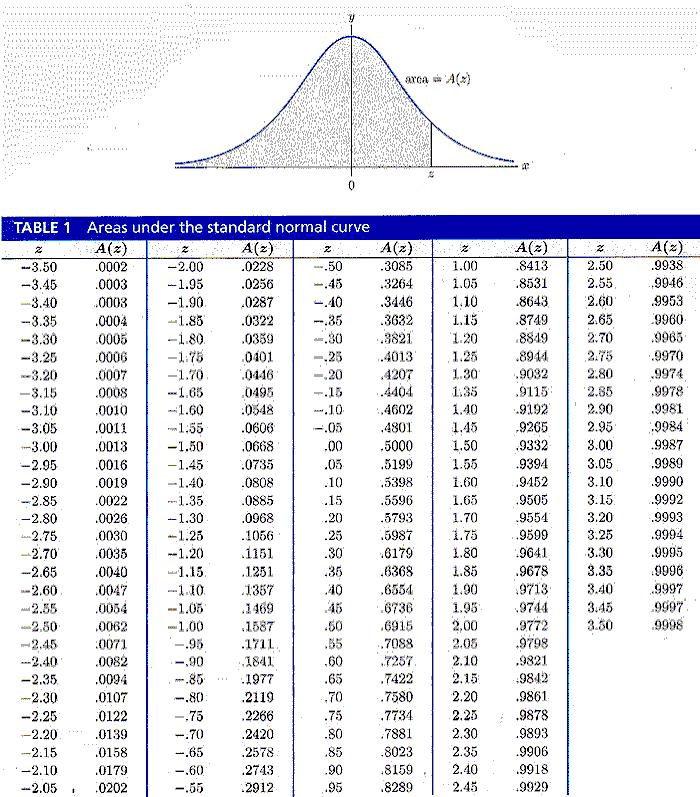
Using the negative Z score table, we find that the proportion below -0.75 is approximately 23.97%. Suppose we have Z scores of -0.75 and 1.25. Therefore, the cut-off point would be around 1.65 standard deviations above the mean. By using the positive Z score table, we find that a Z score of approximately 1.65 corresponds to a cumulative probability of 0.9505. This means that approximately 10.56% of the data falls below a Z score of -1.25. Using the negative Z score table, we locate the corresponding value, which is 0.1056.
We want to find the probability of observing a value less than a Z score of -1.25.
Example 1 - Probability Calculation: Suppose we have a dataset with a normally distributed variable.To solidify our understanding, let's consider a few practical examples: